Last Updated: May 9, 2025

Physics Short Notes

Reference: Ankur Sir

Writer Info:

Jay Prakash

Page Count:

File Size:

Format:

Text

Language:

English

This is the text version of the file "Physics Notes by Ankur Sir", but the product link for "Physics Short Note: Formula Revision" is not available; instead, you can refer to the original PDF from which this short note was created.

Introduction:

In General Science, we study three core subjects: Physics, Chemistry, and Biology. If you are preparing for any competitive exam, whether it is SSC (Staff Selection Commission), RRB (Railway Recruitment Board), or any other one-day exam, Physics holds significant importance.

If your exam is approaching soon and you need a quick revision, this section is for you. It highlights key points and Physics important formulas essential for rapid revision, carefully selected from the Physics Notes PDF file.

Physics Short Note:

Electricity

The size of an atom is measured in Angstrom (Å).

1 Å = 10^{- 10} m

Where: Å = Angstrom

The size of the nucleus is measured in the Fermi meter (fm).

1 f m = 10^{- 15} m

Where: fm = fermi meter

Electric Potential

The work done to bring a unit positive test charge from infinity (∞) to a point in an electric field is called electric potential at that point (P).

Electric potential formula:

V = \frac{W}{q_{0}}

Where: V = Electric Potential; W = Work Done; q₀ = Unit Positive Charge

The unit of electric potential is joule per coulomb or volt.

\frac{J o u l e (J)}{C o u l o m b (C)} = V o l t (V)

Potential difference formula:

Δ V = V_{A} - V_{B} = \frac{W}{q}

Where: ΔV = Potential Difference; V_A = Higher Potential; V_B = Lower Potential; W = Work; q = Charge

Note: The formula for electric potential and potential difference is the same.

Electric Current

The flow rate of electric charge in a particular direction is called electric current.

Electric current formula:

I = \frac{Q}{t}

Where: I = Electric current; Q = Charge; t = Time

The unit of electric current is Coulomb per second or Ampere (A).

\frac{Coulomb (C)}{Second (s)} = Ampere (A)

Note:

Current flow from higher potential to lower potential.
The electric current flows in the opposite direction of the flow of electrons.
For a flow of electric current., there should be a potential difference across the ends of the wire.

Electric Resistance

It is the property of a material that opposes the current flow, determining how difficult it is for electrons to move through it.

Formula:

R = \frac{ρ \times L}{A}

Where: ρ = Resistivity; R = Resistance; L = Length of wire; A = Cross-sectional area

The unit of Resistance is ohms (Ω).

Resistivity

Depends on material and temperature. It does not depend on the length or cross-sectional area. its value remains constant for specific materials.

Resistivity formula:

ρ = \frac{R \times A}{L}

Where: ρ = Resistivity; R = Resistance; L = Length of wire; A = Cross-sectional area

The unit of resistivity is ohm-meter (Ω-m).

Conductance

The ability of a material to allow the flow of electric current through it. It is the inverse of resistance and measures how easily electrons can move through a conductor. Conductance is represented by the symbol 𝐺.

The relationship between conductance and resistance is:

G = \frac{1}{R}

Where: G = Conductance; R = Resistance

The unit of conductance is ohm^-1 (Ω^-1) or mho or Siemens.

\frac{1}{o h m} = o h m^{- 1} = Ω^{- 1} = m h o = S i e m e n s

Note: A higher conductance means lower resistance and better current flow.

Conductivity

Ability to conduct electric current, showing how easily electrons flow through it. It is the inverse of resistivity and depends on factors like material composition and temperature.

Conductivity formula:

σ = \frac{1}{ρ}

Where: σ = Conductivity; ρ = Resistivity

The conductivity unit is ohm^-1/meter (Ω^-1/m), mho/meter (mho/m), or Siemens/meter (S/m).

\frac{Ω^{- 1}}{m} = \frac{m h o}{m} = \frac{Siemens}{m}

Temperature Effect on Resistance

Due to an increase in temperature resistance may increase or decrease because it depends on the material.
- For conductor: If the temperature increases (↑) → resistance increases (↑)
- For semiconductors: If the temperature increases (↑) → resistance decreases (↓)

At 0° Kelvin (- 273.15°C), the conductance of the semiconductor becomes zero.

Superconductor: When the resistance of a material becomes almost zero at extremely low temperatures, that material becomes a superconductor.

At 4.2 Kelvin (-268.8 °C)., mercury behaves like a superconductor.

Fuse wire

Low melting point wire.
High resistance (fragile wire).
Made up of Lead (Pb) + Tin (Sn) alloy wire

Combination of Resistance

Series Combination:

Equivalent Resistance formula for series combination:

R_{e q .} = R_{1} + R_{2} + R_{3} + …

Where: R_eq. = Equivalent resistance

Note: Current remains the same but voltage varies.

V = V_{1} + V_{2} + V_{3} + …

Where: V = Electric potential

Parallel Combination:

Equivalent Resistance formula for parallel combination:

R_{e q .} = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}} + …

Where: R_eq. = Equivalent resistance

Note: Current varies but voltage remains the same.

I = I_{1} + I_{2} + I_{3} + …

Where: I = Electric current

Special Note: If ‘n’ number of wires is given, where, n = 1, 2, 3, 4…, and each wire has the same resistance is ‘R’. Then:

For series combination:

n number of resistance connected in series

R_{e q .} = n . R

For parallel combination:

n number of resistance in parallel combination

R_{e q .} = \frac{R}{n}

Ohm’s Law

Valid at constant temperature.
Valid only for conductors.
At a given temperature the ratio of potential difference and electric current remains the same.

\frac{V}{I} = Constant = Resistance (R)

Where: V = Electric potential; I = Electric current

Electric Appliances

They are connected in parallel combination.

Heater wire:

Has a high melting point.
Having high resistance.
Made of Nichrome alloy = Nickel (Ni) + Copper (Cu)

Electric Bulb:

The filament is made of Tungsten.
Have a high melting point.
Having high resistance.
Having high temperature as well.

Important Instrument

Galvanometer:

Used to detect the weak electric current and their direction.
It is connected in a series combination.
It is more sensitive to electric current than Ammeter.

Ammeter:

Used to measure strong electric current.
It is connected in a series combination.
Have low resistance.
For Ideal Ammeter resistance must be zero (R = 0).

Voltmeter:

Used to measure voltage (Potential difference)
It is connected in parallel combination.
Have high resistance.
For Ideal Voltmeter resistance must be infinite (R = ∞).

Rectifier:

Convert AC (Alternating Current) to D.C (Direct Current).

Inverter:

Convert DC to AC

Conversion of Galvanometer into Ammeter

When we connect a low-resistance wire in parallel with a galvanometer, this combination behaves like an ammeter.

Shunt: It is a low-resistance wire connected in parallel with instruments to protect them from heating.

Conversion of Galvanometer into Voltmeter

When we connect a high-resistance wire in a series combination with a galvanometer, this combination behaves like a voltmeter.

Electric Power (P)

The rate of consumption of energy is called electric power.

Electric power formula:

P = V I = \frac{V^{2}}{R} = I^{2} R

Where: P = Electrical Power; V = Electric potential; I = Electric current; R = Resistance

One kilowatt-hour

It is a commercial unit of energy.

1 K W h = 1 unit = 3 .6 \times 10^{6} J o u l e

Formula to find the number of units:

Number of units = \frac{Watt \times Hours}{100}

Note: The S.I. unit of KWh is Joule (J).

Joule’s law of Heating Effect formula:

H = P t = V I t = \frac{V^{2}}{R} \times t = I^{2} R t

Where: H = Heat; P = Electrical Power; t = Time; V = Electric potential; R = Resistance

Motion

Rest and motion are not absolute terms, they are relative terms. For one person something is rest, while for another the same thing may be in motion.

Distance and Displacement

Distance

• Always positive

• Total path length

• The S.I. unit distance is meter (m)

• Scalar quantity (Only magnitude)

s = v \times t

Where: s = Distance; v = Speed; t = Time

Displacement

• Can be positive, negative, or zero

• The shortest distance between two points

• The S.I. unit displacement is meter (m)

• Vector quantity (Magnitude as well as direction)

\vec{s} = \vec{v} \times t

Where: s = Displacement; v = Velocity; t = Time; (🠪) = Represents vector

Example of Scalar quantities:

Speed
Distance
Time
Mass
Energy
Work
Power
Pressure
Electric charge
Electric current
Electric potential etc…

Example of Vector quantities:

Velocity
Displacement
Acceleration
Force
Linear momentum
Angular momentum
Torque
Electric field
Magnetic field etc…

Average Speed Formula:

v_{a v g} = \frac{{Total distance (s}_{t o t a l})}{{Total time (t}_{t o t a l})}

The S.I. unit of average speed is meter/second (m/s).

Average Velocity Formula:

{\vec{v}}_{a v g} = \frac{Total displacement ({\vec{s}}_{_{t o t a l}})}{{Total time (t}_{t o t a l})}

The S.I. unit of average velocity is meter/second (m/s).

Acceleration Formula:

\vec{a} = \frac{Change in velocity (Δ \vec{v})}{Rate or time (t)}

The S.I. unit of acceleration is meter per square second (m/s²).

Reason of Acceleration:

Increase in speed
Decrease in speed
Change in direction

Equation of Motion

These equations are applicable in the case of uniform acceleration (constant acceleration).

▪ 1^st Equation: Velocity-Time equation

v = u + a . t

▪ 2^nd Equation: Displacement-Time equation

s = u . t + \frac{1}{2} a . t^{2}

▪ 3^rd Equation: Velocity-Displacement equation

v^{2} = u^{2} + 2 a . s

Where: u = Initial velocity; v = Final velocity; a = acceleration; s = Displacement; t = Time

Newton’s Laws of Motion:

▪ 1^st Laws of Motion: Law of inertia (Inertia means opposed to change).

I = m r^{2}

The S.I. unit of Inertia is Kg-m².

▪ 2^nd Laws of Motion: Rate of change of momentum.

F = \frac{Δ \vec{P}}{t} = \frac{Δ m . \vec{v}}{t} = m . \frac{Δ \vec{v}}{t} = m . \vec{a}

The S.I. unit of force is Newton (N) or Kg-m/s².

The CGS unit of force is Dyne or gm-cm/s².

1 {Newton = 10}^{5} Dyne

Where: I = Moment of Inertia; m = Mass; r = Distance; F = Force; P = Linear momentum; t = Time; v = Velocity; a = Acceleration

▪ 3^rd Laws of Motion: Action-reaction law.

Equal and opposite forces.

Impulse

In a very short time (∆t), if an external force acts on a body is known as an impulse and it is a change in momentum (∆P).

Impulse formula:

J = Δ P = m . Δ v = F . Δ t

Where: J = Impulse; ∆P = Change in linear momentum; m = Mass; F = Force; P = Linear momentum; t = Time; v = Velocity

Gravitational force formula:

F = G \frac{m_{1} \times m_{2}}{r^{2}}

Where: F = Force; G = Universal gravitational constant; m = Mass; r = Centre distance between two masses

Where; Value of G = 6.67 \times 10^{- 11} \frac{N - m^{2}}{K g^{2}}

Acceleration due to gravity formula:

g = \frac{G M}{R^{2}}

Where: g = Gravity; G = Universal gravitational constant; M = Mass of Planet; R = Radius of Planet

Where;

g_{E a r t h} = 9.8 {m/s}^{2}

g_{M o o n} = \frac{g_{E a r t h}}{6} = 1.63 {m/s}^{2}

Projectile Motion

The formula for Horizontal Range:

R = \frac{u^{2} Sin 2 θ}{g}

Where: R = Horizontal range; u = Speed of an object; g = Gravity; θ = Inclination angle

Hint: For maximum horizontal range, θ = 45°

The formula for Maximum Height:

H = \frac{u^{2} {Sin}^{2} θ}{2 g}

Where: H = Vertical height; u = Speed of an object; g = Gravity

Hint: For maximum height, θ = 90°

Friction

It is the electromagnetic force in nature.
Always oppose the relative motion.

Friction formula for plane surface:

f = μ R

Where: f = Frictional force; μ = Coefficient of friction; R = Normal reaction force

Friction formula for inclined surface:

f = μ R = μ (m g Cos θ)

Where: f = Frictional force; μ = Coefficient of friction; R = Normal reaction force; m = Mass of an object; g = Gravity; θ = Inclination angle

Hint: Put θ = 0° for the Plane surface.

Torque (τ)

The moment of force is called torque.

Torque formula:

τ = F \times r

Where: τ (tau) = Torque; F = Force; r = Perpendicular distance

The S.I. unit of torque is Newton-meter (N-m).

Angular Momentum Formula:

J = I ω

Where: J = Angular momentum; I = Moment of Inertia; ω = Angular velocity

The S.I. unit of angular momentum is Kilogram-meter per second (Kg-m²/s).

Work, Power & Energy

Mechanical Work

It is a scalar product (dot product) of force and displacement.

Work formula:

W = \vec{F} \cdot \vec{s} = FsCos θ

Where: W = Work; F = Force; s = Displacement; θ = Angle between force and displacement

The S.I. unit of Work is Newton-meter (N-m) or Joule (J).

Work can be positive, negative, or zero.
Work done by a force in circular motion is always zero.
W = mgH, in case of vertical displacement by any object.

As per 3^rd equation of motion:

W = \frac{1}{2} m (v^{2} - u^{2})

Where: W = Work; m = Mass of an object; v = final velocity; u = initial velocity

Hint: valid when θ = 0°

Mechanical Power

The rate of doing work is called mechanical power.

Power formula:

P = \frac{W}{t}

Where: P = Mechanical power; W = Work; t = Rate or time

Note: 1 Horse Power (H.P) = 746 Watt

The S.I. unit of Power is Joule/second (J/s) or Watt.

Another formula of Power:

P = F \times v

Where: P = Power; F = Force; v = Velocity

Energy

Energy can neither be created nor be destroyed, it can only change its form.

The S.I. unit of any form of Energy is Joule (J).

Kinetic Energy Formula:

K . E = \frac{1}{2} m v^{2}

Where: m = Mass; v = Velocity

The kinetic energy in terms of linear momentum (formula):

K . E = \frac{P^{2}}{2 m}

Where: P = Linear momentum; m = Mass

Potential Energy Formula:

P . E = m g h

Where: m = Mass; g = Gravity; h = Vertical height

Note: Formula for Potential Energy of Spring:

P . E = \frac{1}{2} K x^{2}

Where: K = Spring constant; x = Compressed or elongated distance

Heat

Temperature conversion formula:

\frac{° C}{5} = \frac{° F - 32}{9} = \frac{K - 273.15}{5}

Where: ℃ = Degree Centigrade; ℉ = Degree Fahrenheit; K = Kelvin

Important Points:
- Normal human body temperature = 37 ℃ or 98.6 ℉ or 310.15 K
- -40 ℃ = -40 ℉
- Minimum possible temperature = 0 Kelvin or -273.15 ℃ or 459.67 ℉
- Absolute zero temperature = 0 Kelvin
- At 0 Kelvin temperature, the vibration of an atom freezes.

Heat

It is a form of energy whose S.I. unit is Joule (J).

There are two types of heat in nature: Latent heat and Sensible heat.

Latent Heat: All heat energy goes into state (solid, liquid, and gas) change with no change in temperature.

Latent Heat Formula:

Q = m (L . H)

Where: Q = Heat; m = Mass of substance; L.H = Latent Heat

The S.I. unit of Latent Heat is Joule per Kg (J/kg).

Sensible Heat: The state remains the same with temperature change.

Sensible Heat Formula:

Q = m c Δ T

Where: Q = Heat; m = Mass of substance; c = Heat capacity; ∆T = Change in temperature

Note: The S.I. unit of Heat Capacity (c) is Joule/Kg-Kelvin.

Light

Reflection of Light:

For reflection object must be opaque.

For plane surface:

i + g = r + g = 90 °

Where: i = Angle of incidence; r = Angle of reflection; g = glancing angle

Laws of Reflection:
- The incident ray, normal, and reflected ray always lie in the same plane.
- The angle of incidence (i) is always equal to the angle of reflection (r).

Angle of Deviation formula:

δ = 180 ° - 2 i

Where: δ = Angle of deviation; i = Angle of incidence

Plane Mirror:

The plane mirror is neither converging nor diverging therefore Power of the plane mirror is zero.
The focus of the plane mirror is at infinity, therefore focal length is also infinite.
The radius of curvature of the plane mirror is infinite.
Magnification (m) of a plane mirror: m = +1
Magnification (m) will be positive if the image formed is Erect and Virtual.
Magnification (m) will be negative if the image formed is Inverted and Real.

Important Point for Plane Mirror:
- Focal Length: f = ∞
- Focus: F = ∞
- Radius of curvature: R = ∞
- Power of Plane minor: P = 0
- Magnification: m = +1
- Nature of image: Erect and Virtual

Refraction of Light:

When Light enters from one transparent medium to another transparent medium, this event is called as refraction of light.

Example:
- Liquid is Rarer than solid.
- Water is rarer than glass.

Rarer to Denser: Incident ray reflected toward Normal.

Denser to Rarer: Incident ray reflected away from Normal.

Laws of Refraction:

Incident, normal, and refracted rays always lie in the same plane.

Snell’s law: The ratio of Sin(i) and Sin(r) remains constant called the refractive index of medium 2 with respect to medium 1 and represented by the letter ‘n’.

Refractive index formula:

n = \frac{Sin (i)}{Sin (r)} = constant

Where: n = Refractive index; i = Angle of incidence; r = Angle of reflection

Note: Refractive index is a unitless quantity.

Absolute refractive index formula:

n = \frac{c}{v}

Where: n = Refractive index; c = Speed of light in vacuum; v = Speed of light in medium

Total Internal Reflection (TIR):

TIR is possible only when light enters from a denser to a rarer medium.

When the angle of refraction (r) is 90°, the angle of incidence (i) is called critical angle.

When the angle of incidence (i) is greater than the critical angle(i_c) then TIR occurs.

Example of TIR:
- Shinning of diamonds
- Formation of mirage
- Optical Fibre
- Endoscopy

Rainbow:

Reason of formation:
- Dispersion of Light (splitting of white light into seven colors (i.e., VIBGYOR) is called dispersion of Light.)
- Total internal Reflection
- Refraction

Lens and Mirror

Mirror:

Works on the law of reflection.

For all types of mirror: Angle of incident (i) = Angle of reflection (r)

Types of Mirrors:
- Plane Mirror
- Spherical Minor
  - Concave Mirror (converging mirror)
  - Convex mirror (diverging mirror)

Mirror Formula:

\frac{1}{f} = \frac{1}{v} + \frac{1}{u}

Where: f = Focal length; u = Object distance from pole; v = Image distance from pole

Note:

Sign convention for Mirror:
- Focal Length (f)
  - Positive (+) for convex mirror
  - Negative (-) for concave mirror
- Object distance (u)
  - Always negative (-) because an object lies on the left side of the mirror.
- Image distance (v)
  - Positive (+) for convex mirror
  - For the concave mirror, it depends on the object’s location.

Magnification Formula for Mirror:

m = \frac{- v}{u} = \frac{h_{i}}{h_{o}}

Where: m = Magnification of mirror; u = Object distance from pole; v = Image distance from pole; h_i= image height; h_o = Object height

Concave Mirror:

The magnification of a concave mirror can be greater than one (m > 1), less than one (m < 1), or equal to one (m = 1).

Use of Concave Mirror:
- Saving Mirror
- Dentist
- Head Light
- Solar furnace
- Search Light/ Torch
- Solar cooker
- Head Mirror of ENT Doctor
- Reflector Telescope

Convex mirror:

All images by convex mirror are Erect, Virtual & Diminished
Magnification of Convex mirror: m < (+1)
For any position of the object: The image will be Erect (m = +) and Diminished (m < 1).

Uses of Convex Mirror:
- A view finding mirror of vehicles (side mirror / Rearview minor)
- Mirror used in sharp turns
- Mirror used in ATM
- Street Lights

Lens:

The lens works on the law of refraction.

Types of lenses:

Concave lens (Diverging)

Convex lens (Converging)

Lens Formula:

\frac{1}{f} = \frac{1}{v} - \frac{1}{u}

Where: f = Focal length; v = Object distance; u = image distance

Magnification formula for lens:

m = \frac{v}{u} = \frac{h_{i}}{h_{o}}

Where: m = Magnification of lens; v = Image distance; u = Object distance; h_i= image height; h_o = Object height

Power of Lens:

P = \frac{1}{f}

Where: P = Power of lens; f = Focal length

Note: The S.I. unit of Power of lens is Dioptre (D).

The power of the lens is positive (+) for the convex lens and negative (-) for the concave because focal length (f) is positive (+) for the convex lens and negative (-) for the concave lens.

Eye Defects:

Nature of Image at Retina_Real and Inverted_web

Myopia [Near / Short Sightedness]:
- Near objects are visible.
- Distant objects are not visible.
- A concave lens is used to correct myopia.

Hypermetropia [Far / Long Sightedness]:
- Near objects are not visible.
- Distant objects are visible.
- Convex lens is used to correct myopia.

Presbyopia:
- Near and Distant objects are not visible.
- A bifocal lens is used to correct presbyopia.

Astigmatism:
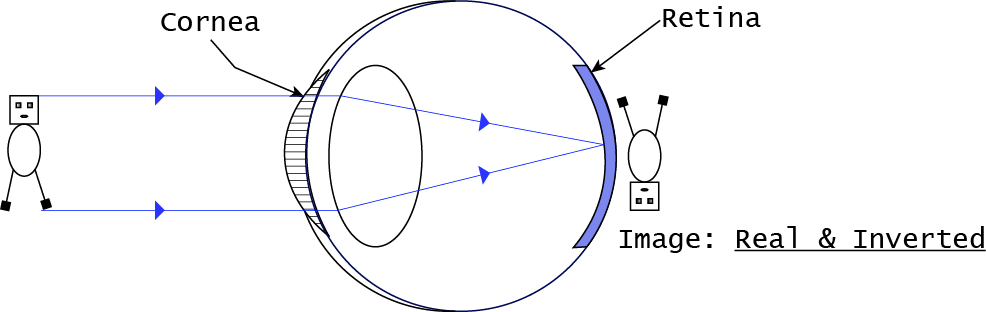
- In this defect, images do not form at a single point and these images are in curve form, the reason behind this defect is distortion in the cornea.
- A cylindrical Lens (Toric lens) is used to correct Astigmatism.

Important note:
- We use Flint glass to make lenses.
- The nature of the image at the Retina of the human eye is Real & Inverted.
- Persistence of eye vision is 1/16 second.
- Air bubbles inside water behave like a concave lens.
- Water drops behave like a convex lens.
- Human eyes behave like a camera of 576 megapixels.

Satellite

If we consider:
- v = Object speed
- v_o = Orbital speed (Circular Path)
- v_e = Escape velocity

Case	Path of Motion
v < v_o	Parabola
v ≥ v_o	Circular or elliptical
v ≥ v_e	Hyperbolic

Orbital speed formula:

v_{o} = \sqrt{\frac{G \times M_{e}}{R_{e} + h}}

Where: G = Gravitational constant; Me = Mass of Earth; Re = Radius of Earth; h = Height of object from the surface of Earth.

Note: If the object is near the earth’s surface, we consider h ≅ 0. Then we consider the orbital formula as given below:

v_{o} = \sqrt{\frac{G \times M_{e}}{R_{e} + 0}} = \sqrt{\frac{G \times M_{e}}{R_{e}}}

Note: The value of orbital speed does not depend on the satellite’s mass.

Escape velocity formula:

v_{e} = \sqrt{2} \times v_{o}

Where: v_e = Escape velocity; v_o = Orbital speed

Note: The ratio of escape velocity to the orbital speed is √2:1.

Note: The value of escape velocity does not depend on the mass of an object.

Kepler’s law of Planetary motion:

1^st Law (Law of Orbits): “All planets around the sun revolve in an elliptical path having sun one of its foci.”

2^nd Law (Law of Arial Speed): “The line joining any planet to the sun sweeps out an equal area in equal time, i.e., the areal speed of the planet remains constant.”

3^rd Law (Law of Periods): “The square of the Orbital periods of the planets are directly proportional to the cubes of the semi-major axes of their orbits”

T^{2} \propto r^{3}

Where: T = Orbital period; r = Semi-major axis

Note: For numerical solving, remember this formula:

\frac{T_{1}^{2}}{T_{2}^{2}} = \frac{r_{1}^{3}}{r_{2}^{3}}

Important Note:
- The total energy of a satellite which is revolving around a planet is always negative.
- Reason for an atmosphere on Earth:
  - The gravitational force of the earth.
  - High escape velocity.
- Kepler’s 2^nd law is based on the law of conservation of angular momentum.`

Matter

Five States of matter are:
- Solid
- Liquid
- Gas
- Plasma
- Bose-Einstein Condensate

Pressure formula:

P = \frac{F}{A}

Where: F = Force; A = Cross-sectional area

Note:
- The S.I. unit of Pressure is Newton per square meter (N/m²) or Pascal (Pa).
- 1 Pascal = 1 N/m²
- Pressure always acts perpendicular to the surface.

Pressure applied by a fluid:

P = ρ g H

Where: P = Pressure; ρ = Density of fluid; g = acceleration due to gravity; H = Height of a point from the free liquid surface

Archimedes’ Principle:
- The weight of an object is felt less inside water.
- The weight of an object decreases inside water, as much as the fluid is displaced.
- Actual weight = Apparent weight + Weight of displaced fluid
- Loss in weight = Weight of displaced fluid.
- The weight of an object will decrease as much as the buoyant force will act on it.
- Loss in weight = Buoyant Force (also called upthrust or thrust)

Pascal Law:
- The pressure applied at any part of a fluid equally transmits at each part of that fluid.
- Hydraulic Brake and Hydraulic lift work on a principle of Pascal’s law.
- In the case of static fluid, pressure at different points in the same horizontal Level will be the same.

Bernoulli’s Theorem:

Applicable on flowing fluids

Bernoulli’s Equation:

P + \frac{1}{2} ρ v^{2} + ρ g H = constant

Where: P = Pressure; ρ = Density; v = Velocity; g = Gravity; H = Height

Note: Bernoulli’s theorem works on the “Law of conservation of energy”.

Surface Tension:

Liquid molecules tend to stick together and form a thin layer (Like a membrane) on the surface of the liquid.
Mosquitoes, Insects, etc can sit on water because of surface tension.
Kerosine oil or detergent powder is used to reduce the value of surface tension.
Surface tension decreases with an increase in temperature.
Raindrops become spherical due to surface tension.
Surface tension occurs due to cohesive force.

Cohesive Force: The forces between the molecules of the same substance are called cohesive forces.
Adhesive Force: The forces between the molecules of different substances are called adhesive force.

Viscosity:

Friction between fluid layers is called viscosity.

Viscous force formula:

F_{v} = 6 π η r v_{T}

Where: F_v = Viscous force; η = Coefficient of viscosity; r = Radius of an object; v_T = Terminal velocity

Note: The S.I. unit of viscosity (η) is Newton-second per square meter (N-s/m²).

Magnetism

Natural Magnet

A natural magnet made from an iron ore called magnetite (Fe₃O₄).
Unlike poles attract each other while Like poles repel each other.
Monopole does not exist. No matter how many parts a magnet is broken into, it will always have two poles (i.e.; North pole & South pole).

Magnetic field

It is a region in space around a magnet, where the force of magnetism can be detected.
Direction of Magnetic line of force:
- Outside Magnet: North to South
- Inside Magnet: South to North
Two magnetic Lines of force never cut each other.
Any point on the magnetic line of force gives the direction of a magnetic field.
The magnetic field is a vector quantity.
The S.I. unit of magnetic field strength is Tesla or Weber/meter².
The CGS unit of magnetic field strength is Gauss.
Current-carrying conductors generate the magnetic field.

Magnetic field formula:

Δ B = K \frac{I (Δ L) Sin θ}{r^{2}}

Note:

K = \frac{μ_{0}}{4 π} = 10^{- 7} \frac{Newton}{A m p e r e^{2}}

Where: μ₀ = Permeability of free space

Where: B = Magnetic field; I = Electric current; L = Length of wire; r = Distance of any point from wire

Force on a current-carrying conductor in a magnetic field (formula):

F = B I L Sin θ

Where: B = Magnetic field; I = Electric current; L = Length of wire; θ = Angle between another magnetic field and current carrying conductor

Force on a charged particle in a magnetic field (formula):

F = q v B Sin θ

Where: q = Charge particle; v = Velocity; B = Magnetic field

Force on a charged particle in electric field (formula):

F = q E

Where: q = Charge particle; E = Electric field

Fleming’s Left-hand Rule

Used in electric motors.
They are used to find the direction of force acting in an electric motor.

Fleming’s Right-hand Rule

Used in an electric generator.
Used to find the direction of induced current.

Wave

A wave occurs due to disturbance in any medium.

Types of Waves

Electromagnetic waves:

They do not require any material medium to travel, i.e., they can travel even in a vacuum.

Only transverse.

Examples: Radio waves, Microwave, Infrared waves, Visible light, Ultraviolet rays, X-rays, γ-rays

Light is an example of an electromagnetic wave.

Mechanical Waves:

They require a material medium to travel, i.e., they cannot travel in a vacuum.

Types of Mechanical waves:
- Longitudinal waves
  - This wave is generated due to the parallel vibration of particles of medium to the wave direction.
  - But particles of the medium do not travel, only energy transfers from one point to another.
  - Example: Sound wave, Wave in spring
- Transverse Waves
  - This wave is generated due to the perpendicular vibration of particles of the medium.
  - But particles of the medium do not travel from one place to another, only energy transfers from one point to another.
  - Example: Waves in string.

Sound

Density effect on the speed of sound:

Speed of sound in solid \propto \frac{1}{\sqrt{Density}}

Stiffness effect on the speed of sound:

Stiffness \propto Speed of sound

Note: The speed of sound increases with an increase in stiffness.

Frequency

The number of cycles in one second is called frequency.

Frequency formula:

f = \frac{1}{T}

Where: f = Frequency; T = Time in second

Note: The S.I. unit of frequency is Hertz (Hz) or Per second (1/s).

Time Period

The time taken in one complete cycle is called time period.

T = \frac{1}{f}

Wavelength

The distance between two consecutive crests or troughs is called wavelength (λ).
SI unit of wavelength (λ) is a meter.
Another unit can be Angstrom (Symbol- Å), Nano-meter (Symbol- nm), etc.

Amplitude

The maximum displacement from a mean position is called amplitude.

Velocity of a wave (formula)

v = f \times λ

v = \frac{λ}{T}

Where: υ = Velocity of wave; f = frequency; λ = wave length; T = time-period

Audible frequency range

For the human ear: 20 Hz to 20000 Hz
Sound frequency less than 20 Hz: Infrasonic sound
Sound frequency greater than 20,000 Hz: Ultrasonic sound

Loudness of sound

Depends on the amplitude of the vibration of vibrating objects.

Loudness \propto {(Amplitude)}^{2}

The unit of loudness is Decibel (dB) or Bel.

1 Bel = 10 dB

Mach number formula

Mach Number = \frac{Speed of Object}{Speed of Sound}

Note: If Mach number = 1, Speed of an object = Speed of sound.

Energy of Wave (formula)

E = \frac{h c}{λ}

Where: E = Energy of a wave; h = Planck’s constant; c = Speed of light in vacuum

Dispersion of light

The splitting of white light into seven colors is called dispersion of light.

Supersonic objects

If the speed of an object is greater than the speed of sound then the object is called a supersonic object.
If the speed of a missile is between 1.2 to 5 Mach then it is called a supersonic missile.

Missile Range

1.2 to 5 Mach⇒ Supersonic missile
Greater than 5 Mach⇒ Hypersonic missile

Important points:
- For echo minimum distance should be 17.15 meters
- Echo works on the law of reflection of sound.
- Persistence of sound = 1/10 second
- Persistence of eye vision = 1/16 second
- A fathometer is used to find sea depth.
- Full form of SONAR = Sound Navigation And Ranging
- Electromagnetic waves do not have any charge.

Unit and Dimension

Quantity	S.I. Unit	Dimension
Length	Meter (m)	[L] or [M⁰L¹T⁰]
Mass	Kilogram (Kg)	[M] or [M¹L⁰T⁰]
Time	Second (s)	[T] or [M⁰L⁰T¹]
Electric current	Ampere (A)	[A]
Amount of substance	Mole (mol)	[mol]

Conclusion:

It is impossible to cover everything in a single article. No matter how much you study for the exam, it may never feel like enough. The Short Formula section is ideal if you’re short on time and need a quick revision. However, if you have more time to prepare, I highly recommend read entire Physics PDF note.

Your support allows us to share more notes in the future. Every donation helps us stay active and continue providing valuable resources.